11317. K-variance
Consider the variance of the sequence a1, a2, ..., an as
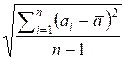
where
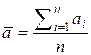
Consider the K-variance as the variance of
the consecutive subsequence of length k.
Your task is to calculate all (n – k
+ 1) K-variances for the given sequence and k.
Formally, the i-th (1 ≤ i
≤ n – k + 1) K-variance ri
is the variance of sequence {ai, ai+1,
..., ai+k-1}.
Input. The first line contains two integers n and k (2 ≤ k ≤
n ≤ 105).
The second line contains n integers
a1, a2, ..., an (|ai| ≤ 100).
Output. Print (n – k + 1) lines with real numbers r1, r2, ..., rn-k+1.
The answer is considered correct if its
absolute or relative error does not exceed 10-4.
|
Sample
input 1 |
Sample
output 1 |
|
3 2 1 3 2 |
1.41421356 0.70710678 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
5 3 1 3 2 4 5 |
1.00000000 1.00000000 1.52752523 |
SOLUTION
mathematics
Algorithm analysis
Let’s
consider the sum:
= 
= 
=
– 
+ 
=
– 
+ 
= – 
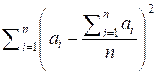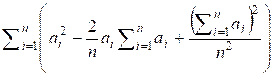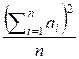Now,
the formula for variance can be rewritten as:
= 
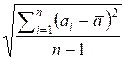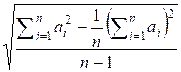
If
we maintain the sum of the elements of the sequence {ai, ai+1, ...,
ai+k-1} (i.e., ai + ai+1
+ ... + ai+k-1) and the sum of their squares (
),
then it is possible to
calculate the desired variance for the segment in constant time.
Example
Let’s
expand the numerator of the fraction in the variance for n
= 3:
+ 
+ 
=
= 
– 
– 
– 
+
+ 
+ + =
= – 
+ 
=
= – 
+ 
=
= – 
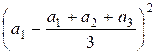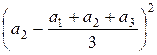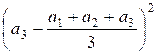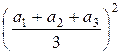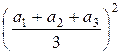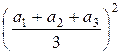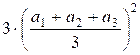Algorithm implementation
Read the
input data.
scanf("%d %d", &n, &k);
a.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &a[i]);
On the
segment [i – k + 1; i] let’s maintain two variables:
·
The
sum sum = ai-k+1 + … + ai-1 + ai,
·
The
sum of squares sum2 = 
sum = sum2 = 0;
Iterate
through the elements of the sequence.
for (i = 0; i < n; i++)
{
Update the
values of sum and sum2.
sum += a[i];
sum2 += a[i] * a[i];
If there is
a window [i –
k + 1; i] of length k, print the result for it.
if (i >= k - 1)
{
printf("%lf\n", sqrt((sum2 - (sum * sum) / k) / (k - 1)));
Remove the
element with index i – k + 1 from the considered sequence.
sum -= a[i - k +
1];
sum2 -= a[i - k + 1] * a[i - k +
1];
}
}